Two key velocity/acceleration transfer theorems#

There are two theorems that are useful in particle kinematics that allow us to compute velocities and accelerations by transferring them to another point. They are discussed below.

Theorem 1: Two-point theorem#

This theorem is useful for determining the velocity (and/or acceleration) of one point on a rigid body by using (or transferring to) another point on the same rigid body.

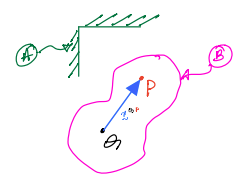
../_images/74.png

In the above figure, \(P\) and \(Q\) are two points that are rigidly fixed to the same rigid body, \(B\). Further, \(B\) is in freemotion relative to \(A\). In other words, \(B\) is moving freely in \(A\); in other words, it is rotating and translating when viewed from \(A\).

In such a scenario, the following two relationships can be used to compute the velocity and acceleration of \(P\) in \(A\).

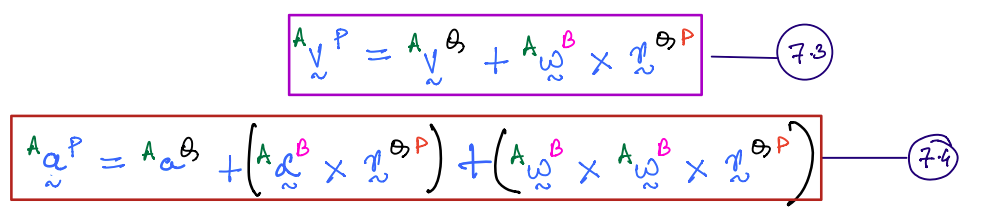
../_images/75.png

where,

../_images/76.png

Some special cases of theorem 1#

Case 1#

If B is purely in translation:

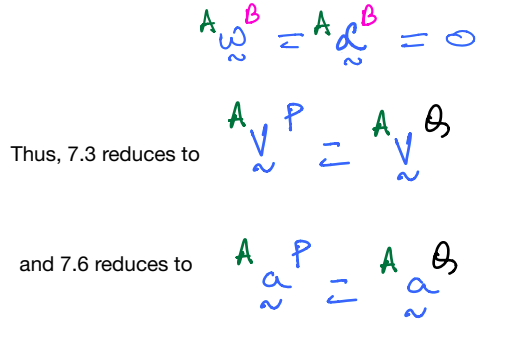
../_images/77.png

Case 2#

If B is in simple rotation about a fixed axis. E.g., a simple pendulum, (see figure).

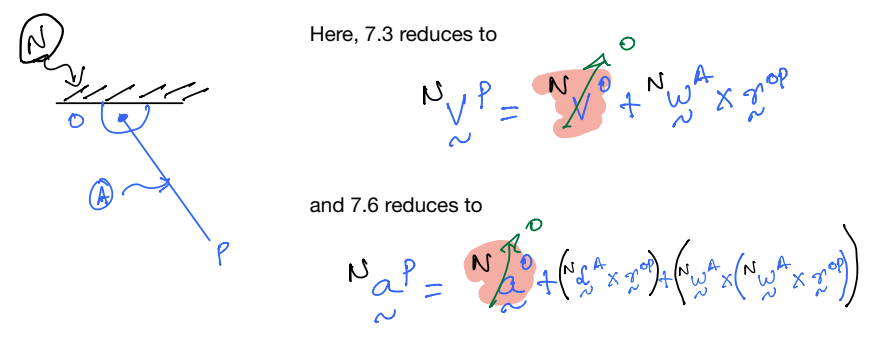
../_images/78.png

Case 3#

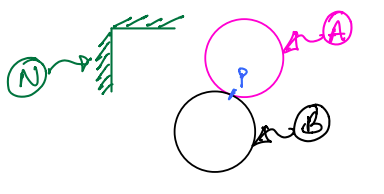
../_images/79.png

Consider the case shown in the above figure containing two discs, \(A\) and \(B\). The two discs are rolling on each other and maintain a single point of contact \(P\). Their motion is observed from a fixed frame \(N\).

As the point \(P\) is clearly shared between the 2 bodies, we introduce the following notation:

  • \(P_A\) is the contact point belonging to body \(A\).

  • \(P_B\) is the contact point belonging to body \(B\).

If it is said that A rolls without slip on B, then the following assumption can be made in tackling a problem:

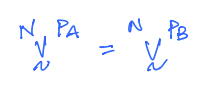
../_images/80.png
Common example for rolling without slip#
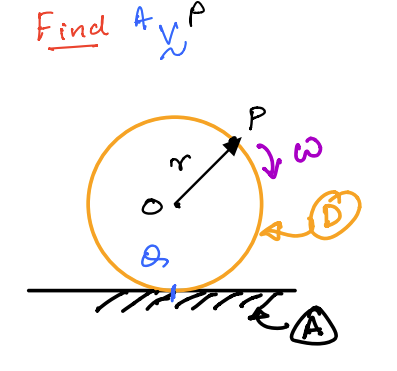
../_images/81.png

In the figure above, the disk \(D\) rolls without slip on \(A\). \(P\) is a point on the disk’s circumference.

Solution

../_images/82.png

Theorem 2: One-point theorem#

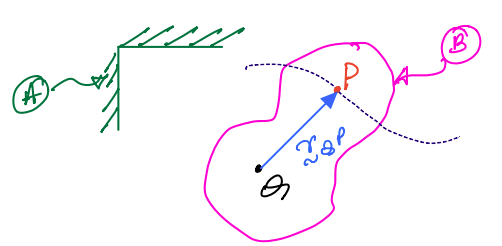
../_images/83.png

In the above figure, \(P\) is a point that translates relative to body, \(B\). Point \(Q\) is rigidly attached to \(B\). The one-point theorem allows computation of the velocity and acceleration of \(P\) relative to the frame \(A\), while accounting for the relative motion of \(P\) as seen from \(B\). The velocity formula is given by Equation \(7.5\).

../_images/84.png

\({}^{B}\vec{v}^{P}\) is the velocity of \(P\) in \(B\). This term is also called relative velocity.

The highlighted term is referred to as coincident point velocity. This highlighted set of terms are identical in form to that seen in the two-point theorem.

The acceleration in this scenario is computed from Equation \(7.6\) (also called five-term beast):

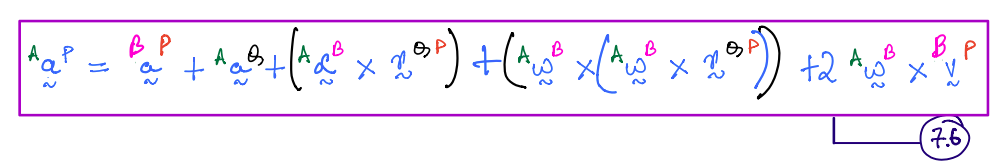
../_images/85.png

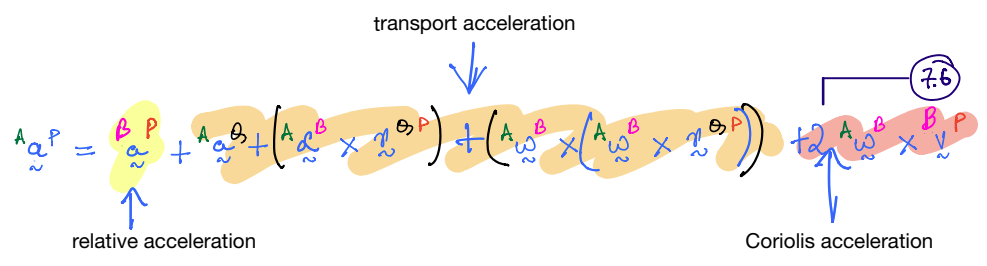
The terms in the acceleration equation have special terminology; these are shown below. Also, note that the ‘transport acceleration’ term below is identical in form to the two-point theorem acceleration formula.

../_images/86.png

Student Activities#

../_images/87.png

  1. Derive relationships \(7.3\) and \(7.4\). You need to make use of key result \(2\) (derivative theorem) and the definitions of velocities and accelerations.

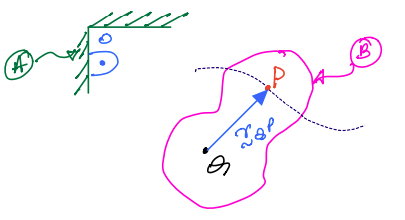
  2. Derive the relationships given by and using the figure below. You will need to draw TWO more position vectors for the derivation. In the figure, \(O\) is rigidly attached To \(A\); \(Q\) is rigidly attached to \(B\); \(P\) moves along a path on \(B\); and \(B\) moves freely relative to \(A\).

  3. Prove that if \(P\) were rigidly fixed to \(B\), then the one-point theorem relations result in the the two-point theorem relationships.

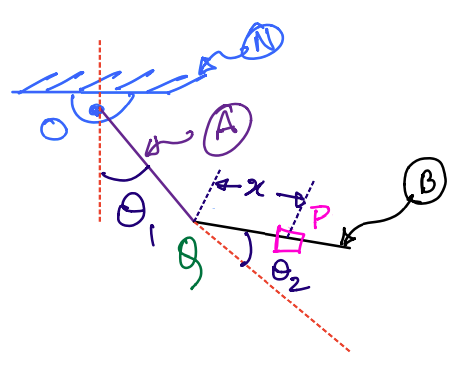
  4. Find: \({}^{N}\vec{v}^{P}\) and \({}^{A}\vec{v}^{P}\) for the particle sliding on the double pendulum using the relevant velocity transfer theorems, as appropriate.

../_images/88.png