Table of Contents
Problem 1: Angular Momentum of a Particle#
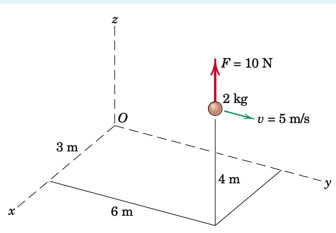
A small sphere has the position and velocity indicated in the figure and is acted upon by the force \(\bf F\); you may ignore this force for now as we will revisit this example in the following week.
Determine the angular momentum of the particle about point O.
You may makes use of all the tools you have learned so far in SymPy to complete your work.
Solution#
The theory#
We have the definition for angular momentum of a generic particle \(P_i\) about \(O\):
\({\bf H}^{P/O} \triangleq {\bf r}^{OP} \times m_{P} ^N{\bf v}^{P}\)
, where:
\({\bf r}^{OP}\) is the position vector from a point \(O\) to \(P\);
\(m_{P}\) is the mass of \(P\); and
\(^N{\bf v}^{P}\) is the velocity of \(P\) with respect to a reference frame \(N\).
So, now, we can turn to the features of sympy to compute the angular momentum.
Computing the solution#
from sympy import symbols, sin, cos
from sympy.physics.mechanics import ReferenceFrame, Point, dynamicsymbols
---------------------------------------------------------------------------
ModuleNotFoundError Traceback (most recent call last)
Cell In[1], line 1
----> 1 from sympy import symbols, sin, cos
2 from sympy.physics.mechanics import ReferenceFrame, Point, dynamicsymbols
ModuleNotFoundError: No module named 'sympy'
N = ReferenceFrame('N')
P = Point('P')
m_P = 2 # mass of P
r_OP = 3*N.x + 6*N.y + 4*N.z
P.set_vel(N, 5*N.y)
N_v_P = P.vel(N)
angular_momentum = r_OP.cross(m_P*N_v_P)
angular_momentum


