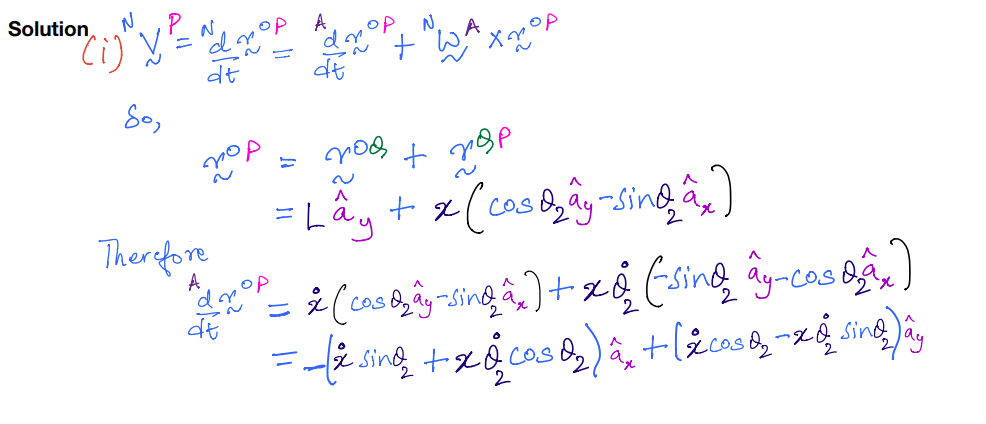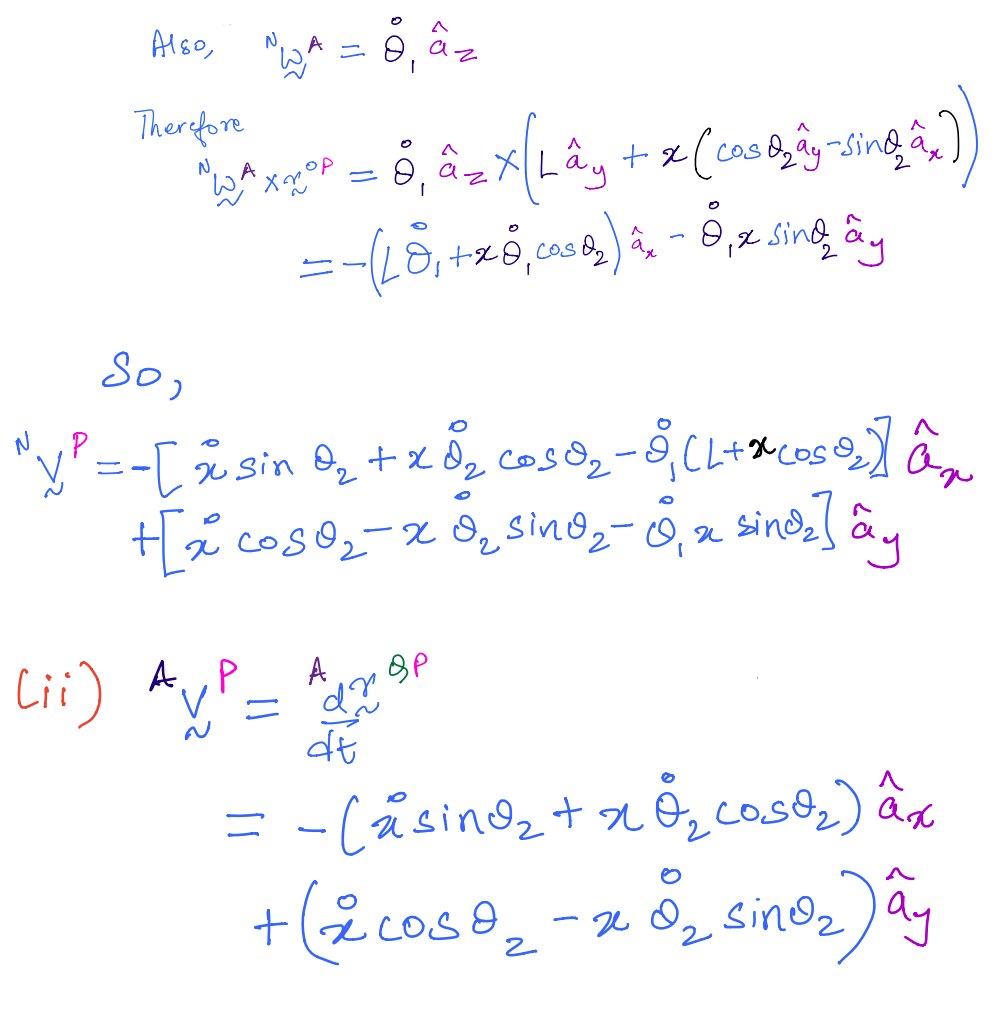Particle Kinematics: Position, Velocity, Acceleration#
So far, we have analyzed changes in orientations of reference frames and the resulting parameters of angular velocity and angular acceleration. In other words, these parameters measure the changes in angles (or angular positions). Now, we will study changes in positions of points. This topic is also called translational kinematics. A pictorial representation of the problem is shown and then described below.
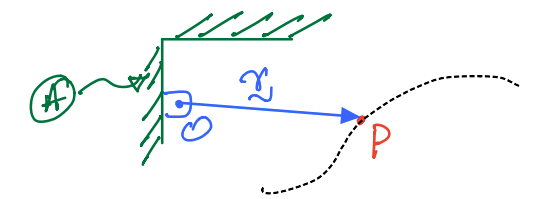
\(O\) is a point rigidly attached to the reference frame \(A\).
\(P\) is a particle of mass \(m\) and is moving along the dashed path. It is said to be translating relative to frame \(A\).
Position of P in A: We utilize \({\bf r}\) a position vector to locate \(P\)-the vector has its tail fixed in \(A\) and its tip (or head) tracks \(P\).
Velocity of P in A: We use the following notation: \({}^{A}{\bf v}^{P}\). Mathematically, the velocity of \(P\) in \(A\) is defined as:

Acceleration of P in A: We use the following notation: \({}^{A}{\bf a}^{P}\). Mathematically, the acceleration of \(P\) in \(A\) is defined as:

or in typeface:
Example#
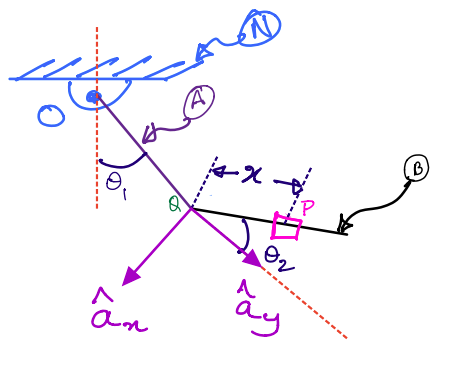
\(N\) is a fixed reference frame to which link \(A\) is attached at a point \(O\). \(B\) is a second link attached to \(A\) at point \(Q\). This system is commonly called a double pendulum. We assume that both links are of the same length \(l\).
\(P\) is a particle that is sliding on \(B\), the second link of the double pendulum. It is located from point \(Q\) by a scalar time-varying parameter \(x\).
The two angles that describe the double pendulum’s two links are also shown in the figure, namely: \(\theta_1\) and \(\theta_2\). You are to compute:
(i) \(^N{\bf v}^P\) and
(ii) \(^A{\bf v}^P\).
Solution