Table of Contents

• 1  Overview of Practice Activity
• 2  Solution
  • 2.1  Evaluate inertia matrix of $A$ about $O$
  • 2.2  Evaluate inertia matrix of $B$ about $O$
  • 2.3  Evaluate inertia matrix of $C$ about $O$
• 3  Generate inertia matrix of system from composite theorem

Overview of Practice Activity

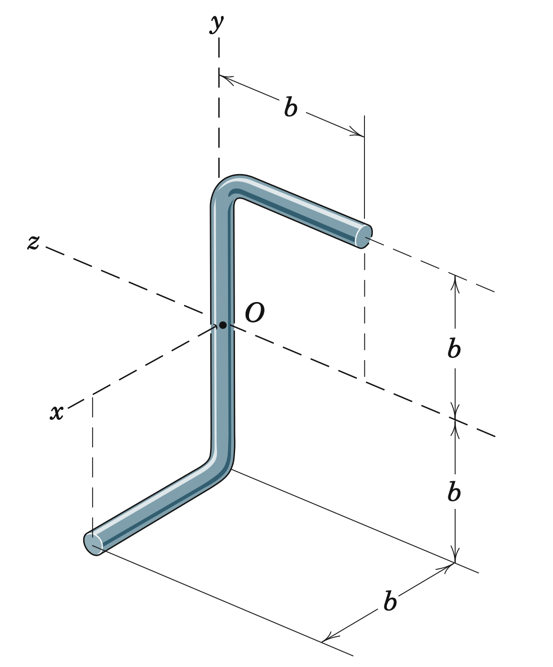
Fig. 13 Door wall

The figure above shows a composite system made up of three slender rods; the total mass of this system is \(M\). For this system, you are to derive the inertia matrix of the system about the point O; that is, determine all the 9 elements of \([{\bf I}]^{S/O}\). Recall that:

\([{\bf I}]^{S/O} = \begin{bmatrix} I^{S/O}_{xx} & I^{S/O}_{xy} & I^{S/O}_{xz} \\ I^{S/O}_{yx} & I^{S/O}_{yy} & I^{S/O}_{yz} \\ I^{S/O}_{zx} & I^{S/O}_{zy} & I^{S/O}_{zz} \end{bmatrix} \)

where the diagonal elements are moment of inertia scalars and off-diagonal elements are product of inertia scalars.

So, your task reduces to calculating each of these terms and assembling it in a matrix using sympy’s Matrix feature.

IMPORTANT: You are to store your inertia matrix solution in the variable name I_matrix_of_S_about_O.

Hints:

1. \(M\) will be useful to determine the mass of individual sections of the composite system.

2. To support your calculations, you are provided the some information regarding the inertia scalars of a slender rod about its mass center (\(G\) in the figure):

Fig. 14 Door wall

The figure above essentially tells you that the moment of inertia scalar about G in a direction perpendicular to rigid rod’s length is \(\frac{1}{12}\)(mass of the rod)\(\cdot\)(length of the rod)\(^2\).

Additionally, you are also told that, for this slender rigid rod in the figure:

• the moment of inertia about G of along its length is zero.

• the products of inertia about G in all directions are all zero.

Solution

from sympy import symbols, Matrix

---------------------------------------------------------------------------
ModuleNotFoundError                       Traceback (most recent call last)
Cell In[1], line 1
----> 1 from sympy import symbols, Matrix

ModuleNotFoundError: No module named 'sympy'

# Create symbols for mass and length
M, b = symbols('M b')

m_A = M/4 # mass of body A
m_B = M/2 # mass of body B
m_C = M/4 # mass of body Cma

Evaluate inertia matrix of \(A\) about \(O\)

I_matrix_of_A_about_A_star = Matrix([
    [m_A*(b**2)/12, 0, 0],
    [0, m_A*(b**2)/12, 0],
    [0, 0, 0]
])
I_matrix_of_A_about_A_star

I_matrix_of_A_star_about_O = Matrix([
    [m_A*(b**2 + (b/2)**2), 0, 0],
    [0, m_A*((b/2)**2 + 0**2), m_A*(b/2)*b],
    [0, m_A*(b/2)*b, m_A*(b)**2]
])

I_matrix_of_A_star_about_O

I_matrix_of_A_about_O = I_matrix_of_A_about_A_star + I_matrix_of_A_star_about_O
I_matrix_of_A_about_O

Evaluate inertia matrix of \(B\) about \(O\)

I_matrix_of_B_about_B_star = Matrix([
    [m_B/12*(2*b)**2, 0, 0],
    [0, 0, 0],
    [0, 0, m_B/12*(2*b)**2]
])

I_matrix_of_B_star_about_O = Matrix([
    [0, 0, 0],
    [0, 0, 0],
    [0, 0, 0]
])

I_matrix_of_B_about_O = I_matrix_of_B_about_B_star + I_matrix_of_B_star_about_O
I_matrix_of_B_about_O

Evaluate inertia matrix of \(C\) about \(O\)

I_matrix_of_C_about_C_star = Matrix([
    [0, 0, 0],
    [0, m_C/12*(b)**2, 0],
    [0, 0, m_C/12*(b)**2]
])

I_matrix_of_C_about_C_star

I_matrix_of_C_star_about_O = Matrix([
    [m_C*(b)**2,          m_C*(b/2)*(b),                       0],
    [m_C*(b/2)*(b),       m_C*(b/2)**2,                        0],
    [0,                       0,          m_C*((b/2)**2 + (b)**2)]
])

I_matrix_of_C_star_about_O 

I_matrix_of_C_about_O = I_matrix_of_C_about_C_star + I_matrix_of_C_star_about_O
I_matrix_of_C_about_O

Generate inertia matrix of system from composite theorem

I_matrix_of_S_about_O = I_matrix_of_A_about_O + I_matrix_of_B_about_O + I_matrix_of_C_about_O

I_matrix_of_S_about_O