Mass/Inertia Scalars

• Mass: the quanity of matter within a given body. The units of measurement are: \(kg\), \(lb\).

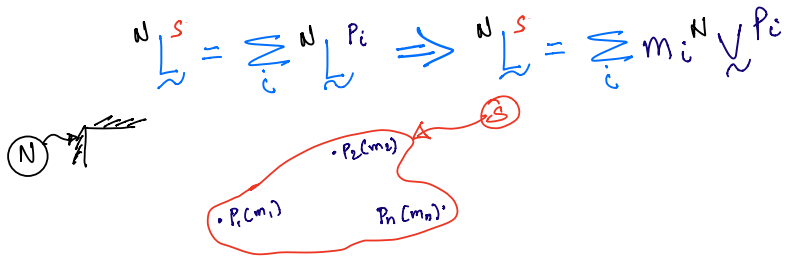
• Mass center: consider a set of particles as shown below which together make up the system of particles \(S\):

The \(i^{\text{th}}\) particle has a mass \(m_i\)

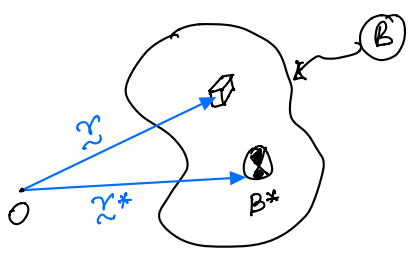
\(S^*\) is a fictitious particle such that:

\[\sum_{i} m_i {\bf p}_i = 0 \tag{8.1}\]

This fictitious particle is called mass center. The mass center can be located by introducing a indipendant point seperate to the body.

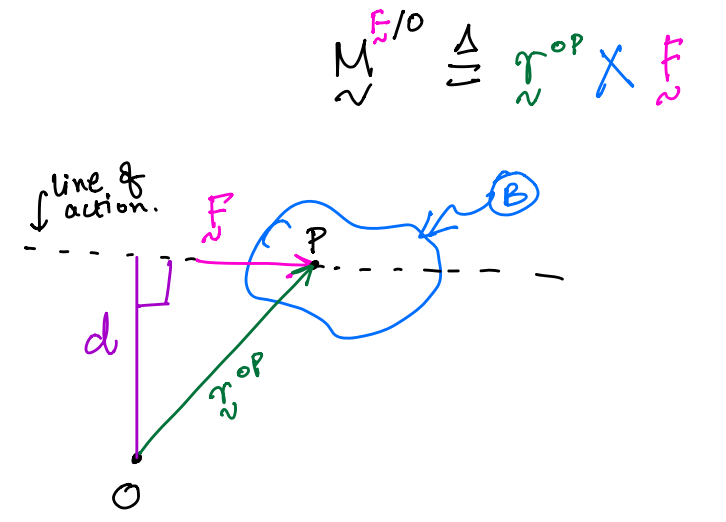
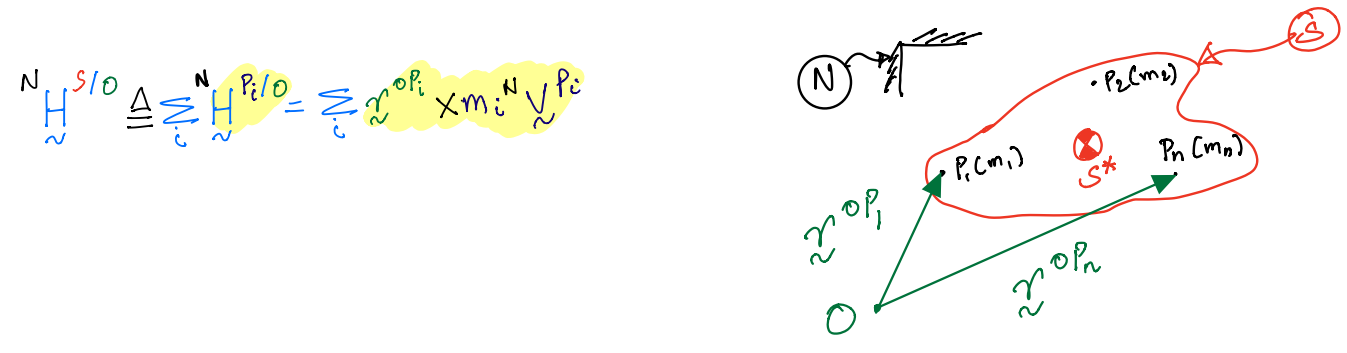
• \({\bf r}^*\); position vector from \(O\) to \(S^*\)

• \({\bf q}_n\); position vector from \(O\) to \(P_n\)

So, the position vector to locate the \(n^{th}\) particle is:

\[ {\bf p}_n = {\bf r}^* - {\bf q}_n \]

Thus, expanding 8.1:

\[\sum_i {m_i}{\mathbf{p}_i} =0\]

\[\rightarrow {m_1}{\mathbf{p}_1} + {m_2}{\mathbf{p}_2} + ... + {m_n}{\mathbf{p}_n} = 0\]

\[\rightarrow {m_1}{{\mathbf r}^* - {\mathbf q}_1} + {m_2}{{\mathbf r}^* - {\mathbf q}_2} + ... + {m_i}{{\mathbf r}^* - {\mathbf q}_n} = 0\]

\[\rightarrow {\mathbf r}^* (m_1 + m_2 + ... + m_n ) = {m_1}{\mathbf{q}_1} + {m_2}{\mathbf{q}_2} + ... + {m_n}{\mathbf{q}_n}\]

\[\rightarrow {\mathbf r}^* = \frac{{m_1}{\mathbf{q}_1} + {m_2}{\mathbf{q}_2} + ... + {m_n}{\mathbf{q}_n}}{(m_1 + m_2 + ... + m_n )}\]

\[{\mathbf r}^* = \frac{\sum_i {m_i}{\mathbf{q}_i}}{\sum_i {m_i}} \tag{8.2}\]

For a continuum:

\[{\mathbf r}^* = \frac{\int {\mathbf r}^* \mathrm{d}m}{\int \mathrm{d}m} = \frac{\int e {\mathbf r}^* \mathrm{d}V}{\int e \mathrm{d}V} \tag {8.3}\]

where, \(\mathrm{d}m\) is elemental mass that can be obtained from density \(\rho\) and elementary volume \(\mathrm{d}V\).

Composite theorem for mass centre

\[{\mathbf r}^* = \frac{{m_{s_1}{{\mathbf{r}_1}^*}} + {m_{s_2}{{\mathbf{r}_2}^*}} + {m_{s_3}{{\mathbf{r}_3}^*}} + ...}{(m_{s_1} + m_{s_2} + m_{s_3} + ...)} \tag{8.4}\]

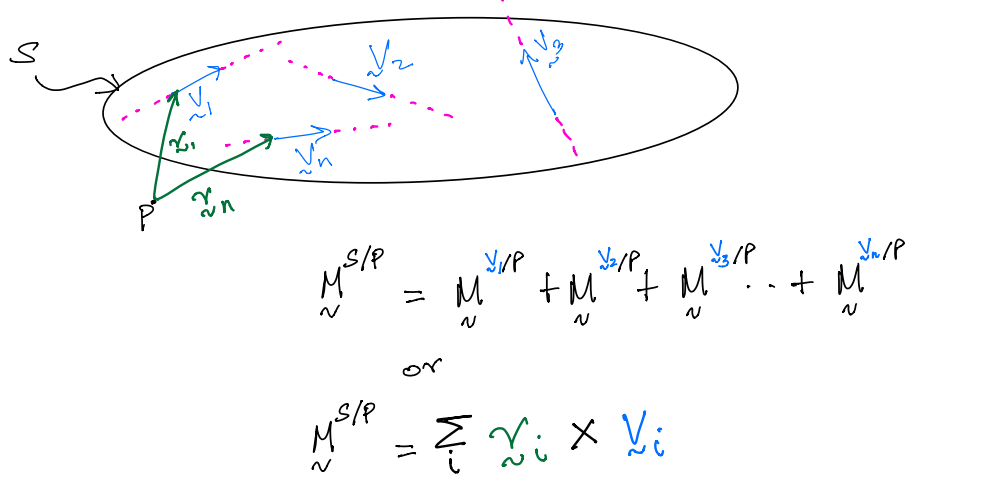
where,

• \(r^*_i\) is the position vector locating the mass centre of \(S_i\), the \(i^{\text{th}}\) system of particles.

• \(m_{s_{i}}\) is the mass of \(i^{\text{th}}\) system.

• \(r^*\) is the mass centre of the composite system \(S\).

Example #1

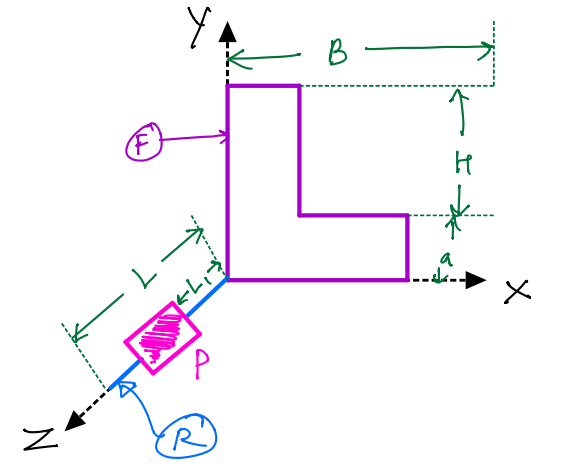
Given:

• \(F\) and \(R\) are the bodies of mass density \(\rho\; kgm^{-2}\) and \(\sigma\;kgm^{-1}\) respectively.

• \(P\) is a particle of mass \(m\).

Find:

• Mass centre of the combined system.

Example #2

\(F\) is split into two: \(F_1\) and \(F_2\).

\(m_{F_{1}}\) = \(\rho H_a\), is mass of \(F_1\).

\(m_{F_{2}}\) = \(\rho B_a\), is mass of \(F_2\).

Also,

\(m_{R}\) = \(\sigma L\), is mass of \(R\).

Then,

\[ X^* = \frac{{m_{F_1}} {\frac{a}{2}} + {m_{F_2}} {\frac{b}{2}} + m_R (0) + m(0)}{m_{F_1} + m_{F_2} + m_R + m} \]

Similarly,

\[ Y^* = \frac{m_{F_1} \left( a + \frac{H}{2} \right) + m_{F_2} \frac{a}{2}}{m_{F_1} + m_{F_2} + m_R + m} \]

and

\[ Z^* = \frac{m_R \frac{L}{2} + m L_1}{m_{F_1} + m_{F_2} + m_R + m} \]

Inertia scalar

For a particle \(P\) of mass \(m\), we can define a parameter called the inertia scalar. This is defined relative to an arbitrary point \(O\). There are two such inertia scalars:

1. Product of inertia

Notation

\(I^{P/O}_{ab}\) is the product of inertia of \(P\) along two lines through point \(O\) that are parallel to unit vectors \(\hat{\bf n}_a\) and \(\hat{\bf n}_b\).

\[ I^{P/O}_{ab} \triangleq m \left( {\mathbf p} \times \hat{\bf n}_a \right) \cdot \left( {\mathbf p} \times \hat{\bf n}_b \right) \tag{8.5} \]

8.5 can be extended for both systems of particles and continua.

Product of inertia of system particles

\[ I^{S/O}_{ab} \triangleq \sum_i m_i \left( {\mathbf p}_i \times \hat{\bf n}_a \right) \cdot \left( {\mathbf p}_i \times \hat{\bf n}_b \right) \tag{8.6} \]

Product of inertia of continua

\[ I^{B/O}_{ab} \triangleq \int \mathrm{d}m \left( {\mathbf p} \times \hat{\bf n}_a \right) \cdot \left( {\mathbf p} \times \hat{\bf n}_b \right) \tag{8.7} \]

Warning

In all cases, \(I_{ab} = I_{ba}\) because the formula relies on the dot product of vectors.

2. Moment of inertia

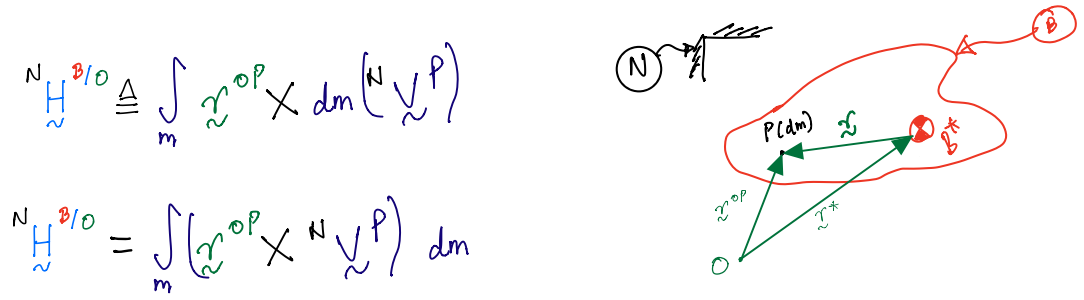
Notation

\(I^{P/O}_{aa}\) is the moment of inertia of P about a line through point \(O\) which is parallel to the unit vector \(\hat{\bf n}_a\).

\[ I^{P/O}_{a} \triangleq m \left( {\mathbf p} \times \hat{\bf n}_a \right) \cdot \left( {\mathbf p} \times \hat{\bf n}_a \right) \tag{8.8} \]

\[ I^{P/O}_{aa} \triangleq m \cdot |{\mathbf p} \times \hat{\bf n}_a|^2\]

\[ = m \left( |\mathbf{p}| \cdot |\hat{\bf n}_a| \cdot \sin\theta \right)^2 \]

\[ = m \left( |\mathbf{p}| \cdot 1 \cdot \sin\theta \right)^2 \]

\[= m d^2\]

8.8 can be extended to both systems of particles and continua.

Moment of inertia of system of particles

\[ I^{S/O}_{a} \triangleq \sum_i m_i \left( {\mathbf p}_i \times \hat{\bf n}_a \right) \cdot \left( {\mathbf p}_i \times \hat{\bf n}_a \right) \tag{8.9} \]

Moment of inertia of a continua

\[ I^{B/O}_{a} \triangleq \int \mathrm{d}m \left( {\mathbf p}_i \times \hat{\bf n}_a \right) \cdot \left( {\mathbf p}_i \times \hat{\bf n}_a \right) \tag{8.10} \]

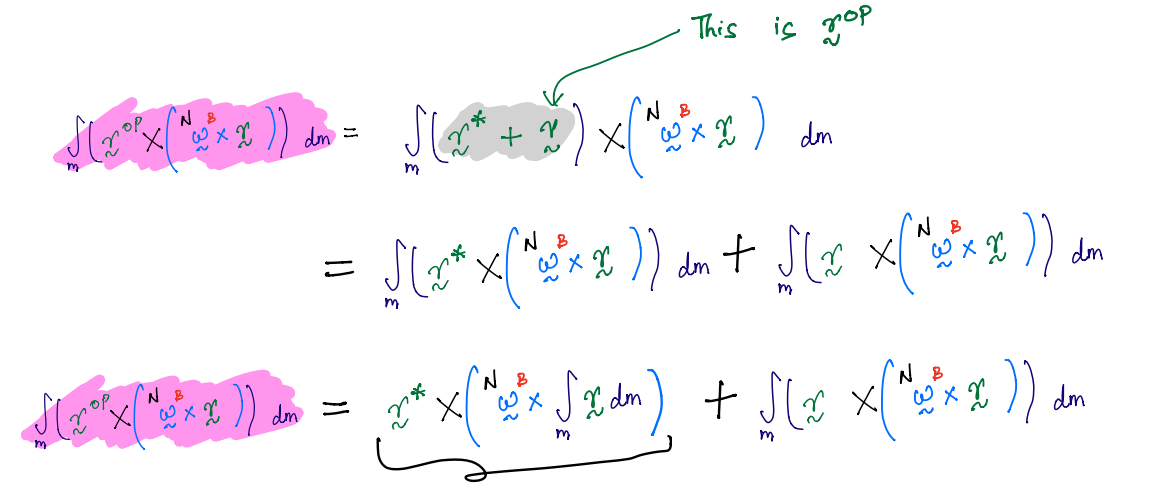
Example

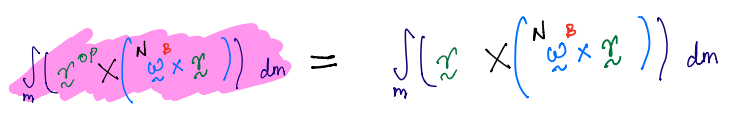
• \(P\) is a particle of mass \(m\).

• \(\hat{\bf n}_x,\;\hat{\bf n}_y,\;\hat{\bf n}_z\) are unit vectors that are mutually orthogonal.

• \({\bf r} = x\hat{\bf n}_x + y\hat{\bf n}_y + z\hat{\bf n}_z\)

Find:

\[ I^{P/O}_{xx} \qquad I^{P/O}_{yy} \qquad I^{P/O}_{zz} \]

Solution

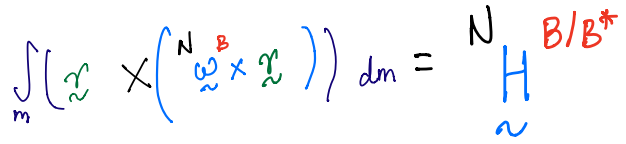
From inertia scalars to inertia matrix

• From the previous example, we now have some insight that we will be interested in computing the moments of inertia and products of inertia about a set of unit vectors that make up a reference frame.

• For this discussion, we assume that the unit vectors are: \(\hat{\bf n}_x,\;\hat{\bf n}_y,\;\hat{\bf n}_z\).

• The inertia scalars can be used to define a square matrix called the inertia matrix.

Notation:

• \(\left[I\right]^{S/O}\) is the inertia matrix of \(S\), a system of particles about the point \(O\).

• The diagonal elements of this matrix are the moments of inertia.

• The off-diagonal elements are the products of inertia.

• So, the inertia matrix is represented as:

\[\begin{split} \left[{I}\right]^{S/O} = \begin{bmatrix} {I^{S/O}_{xx}} & {I^{S/O}_{xy}} & {I^{S/O}_{xz}} \\ {I^{S/O}_{yx}} & {I^{S/O}_{yy}} & {I^{S/O}_{yz}} \\ {I^{S/O}_{zx}} & {I^{S/O}_{zy}} & {I^{S/O}_{zz}} \\ \end{bmatrix} \end{split}\]

Warning

In all cases, \(I_{ab} = I_{ba}\) because the formula relies on the dot product of vectors.

• Rigid body/ continua: The inertia scalars of a rigid body can also be arranged into an inertia matrix.