Forces, Moments, and Torques#

Vectors may or may not have what is called a “line of actions”. This leads to two classifications of vectors:

Bound vector#

A bound vector is a vector that acts along a specific line in space and is associated with a particular point. This means it is “bound” to its line of action and affects that specific point. For example, in the figure below, the force \(\mathbf {F}\) acts on the body \(B\) at a specific point \(P\), which lies on the line of action of \(\mathbf{F}\). Thus, \(\mathbf {F}\) is a bound vector.

../_images/1.png

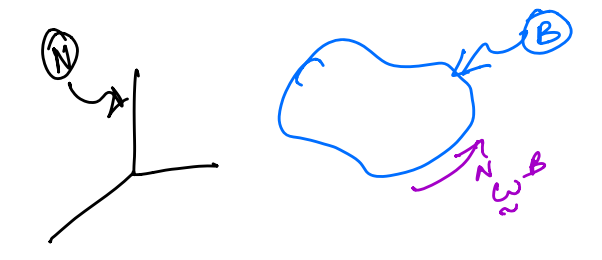
Free vector#

Free (or unbound) vector is a vector that is not bound to a line of action. A good example of this is the angular velocity vector that acts on a body. The angular velocity of a body has a magnitude and direction but does not act at a specific point; this is because the angular velocity is the same at any location on a single rigid body. This is illustrated in the figure below.

../_images/2.png

Moments#

If a vector is classified as a bounded one, then one can define a parameter called the moment for this bound vector about a specific point. For an example of this reflect take the figure below. This figure illitrates a force \(\mathbf{F}\) being exterted on point, \(P\).

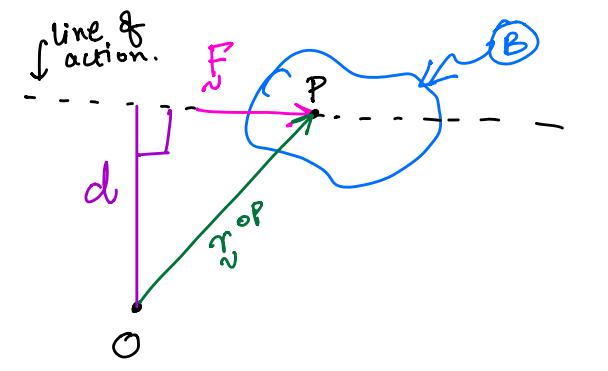
../_images/3_cut.png

When observed from point \(O\), we can define the moment of force \(\mathbf{F}\) about the point \(O\). This is defined mathematically as:

\[\mathbf {M}^{\mathbf{F}/O} \triangleq \mathbf{r}^{OP} \times \mathbf{F}\]

Where,

  • \(\mathbf{r}^{OP}\) is the position vector from \(O\) to \(P\).

  • \(\mathbf{M}^{\mathbf{F}/O}\) is the moment of \(\mathbf{F}\) about \(O\).

The magnitude of this moment can be defined by only taking into account the component of \(\mathbf{r}^{OP}\) perpendicular to \(\mathbf{F}\). It can be determined mathematically as:

\[|{\mathbf {M}^{\mathbf{F}/O}}| \triangleq d |\mathbf{F}|\]

where,

  • \(d\) is the component of \(\mathbf{r}^{OP}\) perpendicular to \(\mathbf{F}\).

From this, we observe that the moment of a force results in a vector. This vector is derived from the cross product of the position vector and the force. It’s important to note that moments do not exist for free vectors.

Resultant of a set of vectors#

Consider \(S\), a set of vectors \(<\mathbf{v}_{1}, \mathbf{v}_{2}, \ldots, \mathbf{v}_{n}>\),

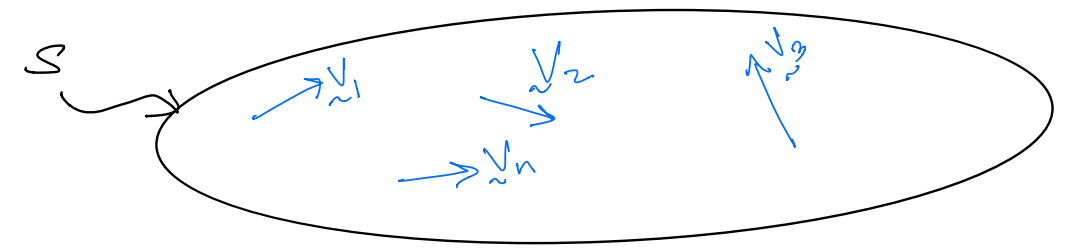
../_images/5.png

The resultant of this set of vectors is the vector sum of the elements of the set.

\[\mathbf{R}=\mathbf{v}_{1} + \mathbf{v}_{2} + \mathbf{v}_{3} + \ldots + \mathbf{v}_{n}\]

If the vectors are bounded, as we saw previously, we can find the moment of the set of vectors about some point \(P\):

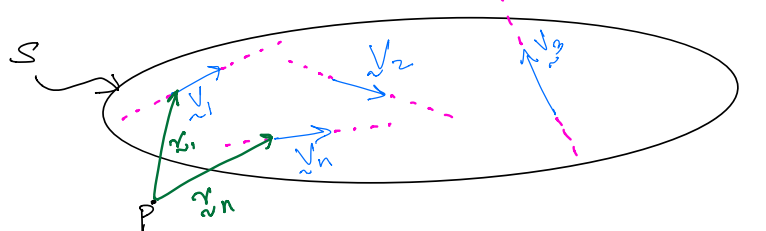
../_images/7_cut.png

The mathmatical defination is given as:

\[\mathbf {M}^{S/P} = {\mathbf{M}^{{\mathbf{v}_1}/P}} + {\mathbf{M}^{{\mathbf{v}_2}/P}} + {\mathbf{M}^{{\mathbf{v}_3}/P}} + {\mathbf{M}^{{\mathbf{v}_n}/P}}\]

A simplified version of writing this is:

\[\mathbf {M}^{S/P} = \sum_i \mathbf{r}_i \times \mathbf{v}_i\]

Note

The set of vectors discussed here can represent any bound vectors, not just forces. However, the principles we’ve developed are especially applicable to forces, since forces are a common example of bound vectors.

A Key Theorem on Moments#

Given a set of vectors and a reference point \(P\) discussed earlier, we can find the moment of this set about another point \(Q\) (see figure below). This can be done using a theorem that involves the resultant vector \(R\) of the set, which is explained below the figure.

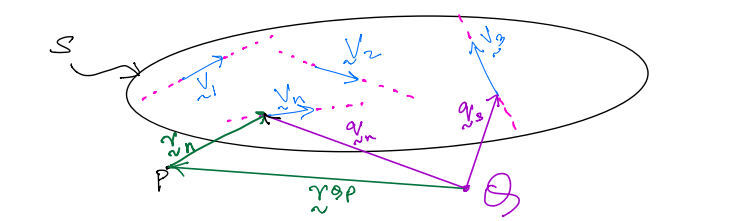
../_images/8_cut.png
\[\mathbf {M}^{S/Q} = \mathbf {M}^{S/P} + (\mathbf{r}^{OP} \times \mathbf{R})\]

Proof:#

\[\mathbf {M}^{S/Q} = \sum_i \mathbf{q}_{i} \times \mathbf{v}_i\]
\[\mathbf {M}^{S/Q} = \sum_i (\mathbf{r}^{QP} + \mathbf{r}_i) \times \mathbf{v}_i\]
\[\mathbf {M}^{S/Q} = (\mathbf{r}^{QP} \times \sum_i \mathbf{v}_i) + \sum_i(\mathbf{r}_i \times \mathbf{v}_i)\]
\[\mathbf {M}^{S/Q} = (\mathbf{r}^{OP} \times \mathbf{R}) + \mathbf {M}^{S/P}\]

Couple#

A set of bound vectors with zero resultant is said to be a couple. A couple is not a vector; it is a set of vectors. A couple can contain as many vectors as needed to satisfy the condition of zero resultant. The minimum number of vectors in a couple is two; this is called a simple couple, where the two components are equal in magnitude and oppositely directed.

Examples#

../_images/9.png

Torque of a couple#

The torque of a coupleis the moment of a couple about an arbitrary point in space. A torque is a vector quantity.

Equivalence#

Equivalence is another important concept in dynamics that applies to sets of vectors. Two sets of vectors, \(\mathbf{S}_1\) and \(\mathbf{S}_2\), are said to be equivalent if and only if:

  • The resultant of \(\mathbf{S}_1\) is identical to the resultant of \(\mathbf{S}_2\).

  • The moment of \(\mathbf{S}_1\) about some point \(O\) is identical to the moemnt of \(\mathbf{S}_2\) about the same point \(O\).

Note

If the sets have the same moments about \(O\), they will have the same moments about any other point, as well.

Replacement#

If we have two sets of bound vectors that are equivalent, then in the context of rigid body dynamics one of the sets can always be replaced by the other equivalent set. In other words, either set of vectors can be called a replacement of the other.

If two couples have equal torques, then they are replacement of each other because:

  • The resultant, \(\mathbf{S}\), of the couples are zero; and

  • They have the same moment (or torque) about any point.

Pictorial example#

Consider the body \(B\) with a point \(P\) with only a set of forces \(<\mathbf{F}_{1}, \mathbf{F}_{2}, \mathbf{F}_{3}, \mathbf{F}_{4}>\) acting on it as shown below:

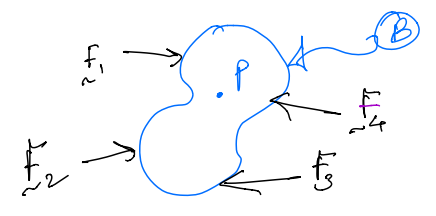
../_images/10.png

These forces can be replaced by another equivalent set; this set consists of:

  • \(\mathbf F\), a single force through \(P\), which has the same resultant as the above set of forces.

  • \(\mathbf T\), a torque of a couple with the same moment about \(P\), as the set of forces \(<\mathbf{F}_{1}, \mathbf{F}_{2}, \mathbf{F}_{3}, \mathbf{F}_{4}>\).

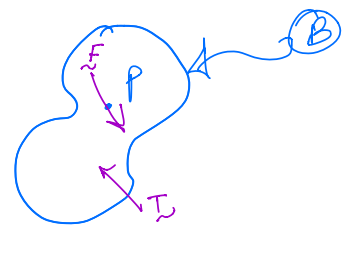
../_images/11_cut.png

So,

\[\sum_i \mathbf{F}_i = \mathbf{F}\]

And,

\[\sum_i \mathbf{M}^{\mathbf{F}/P} = \mathbf T\]

Though we have described everything above in the context of forces and moments of force, the developments apply to vectors more generally. In other words, one set of bound vectors can be replaced by another set; this second set consists of one bound vector (i.e., the resultant of the first set) and a torque of a couple.