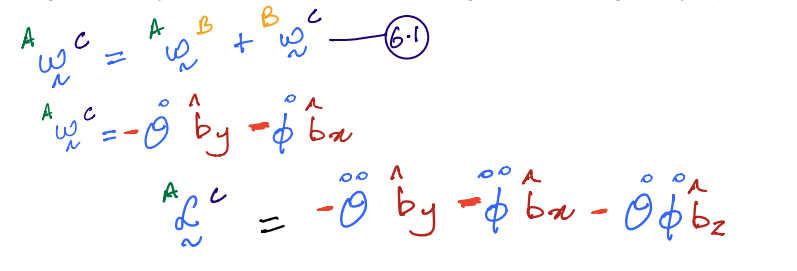Angular Velocity and Angular Acceleration#
Angular velocity#
Angular velocity is defined as the time rate of change of orientation.
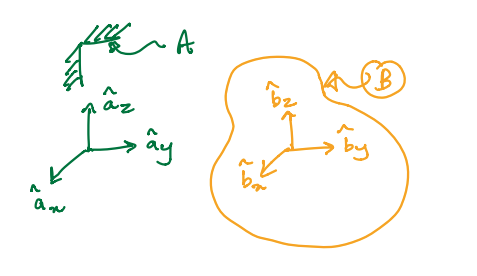
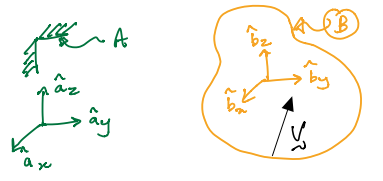
Angular velocity is denoted using the greek letter omega. For example, in the figure below, \({}^{A}{\boldsymbol \omega}^{B}\) is the angular velocity of B in A
Case 1: Simple Rotation#
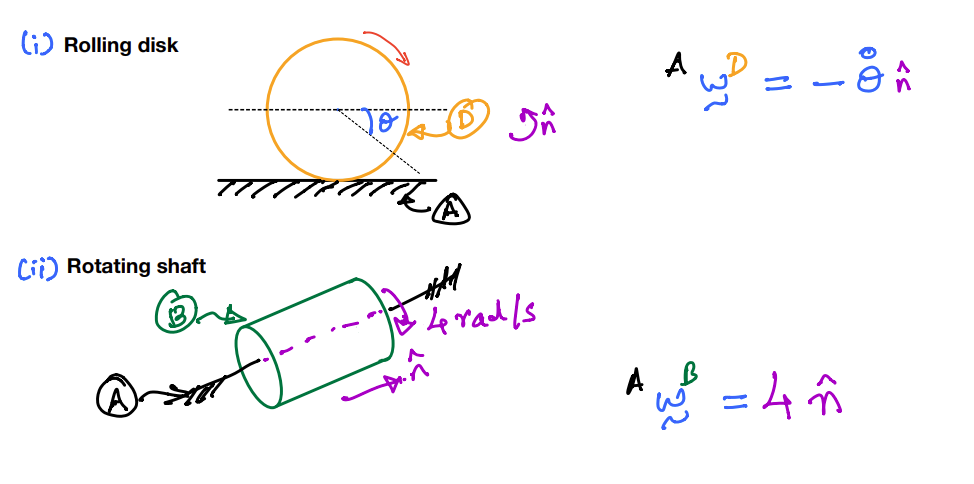
The motion of \(B\) in \(A\) is a simple rotation if and only if there exists a unit vector \(\hat{\bf n}\) that remains fixed in both \(B\) and \(A\) as \(B\) moves in \(A\). Mathematically, simple rotation leads to

Examples#
Case 2: General 3-D Rotation#
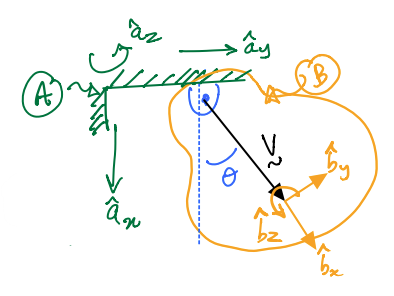
Below, body \(B\) is moving freely relative to frame \(A\).
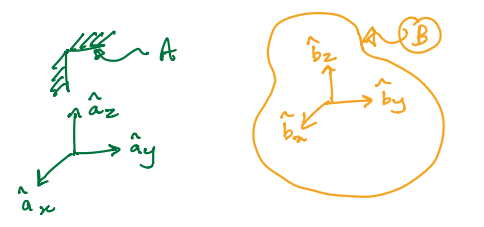
\(\hat{\bf b}_x\), \(\hat{\bf b}_y\) and \(\hat{\bf b}_z\) are rigidly fixed to \(B\).
The angular velocity of body \(B\) in frame \(A\) is mathematically defined as:
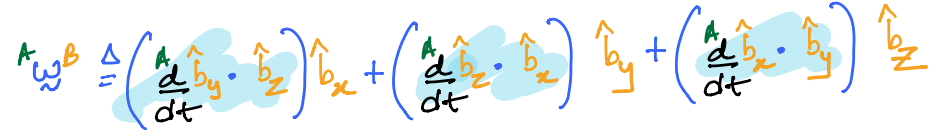
which can then be written in a more compressed form as:

where \(\omega_x,\;,\omega_y,\;\omega_z\) are scalar components of the angular velocity vector in the \(x\), \(y\), and \(z\) directions respectively.
Addition rule for angular velocity (aka Chain rule for angular velocity)#
Given three bodies \(A, B\) and \(C\) that move relative to each other and also a fixed reference frame \(N\), the following rule is provided to compute the \(^N{\boldsymbol \omega}^C\):
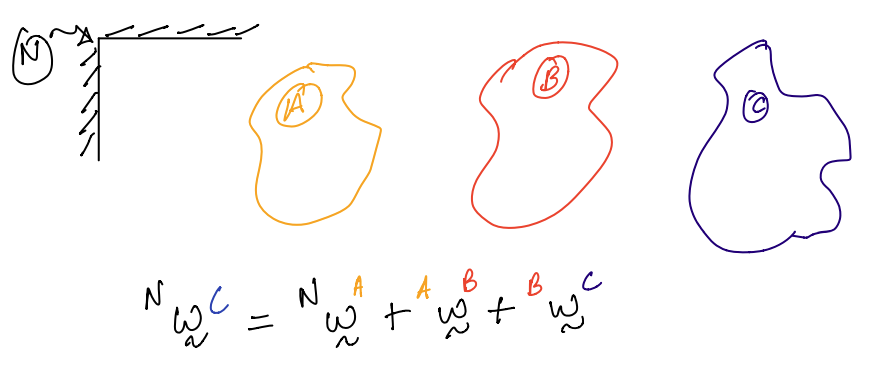
In typeface, this can be written as:
Angular acceleration:#
Angular acceleration is the time rate of change of angular velocity vector.
In the figure above, \(B\) is moving freely in \(A\). The angular acceleration of \(B\) in \(A\) is denoted as \({}^{A}{\boldsymbol \alpha}^{B}\). It is defined as:
Indeed, one must be careful to express the angular velocity in the appropriate reference frame prior to computing its time derivative. Unfortunately, it is not always convenient (or desirable and might even be impossible) to switch between reference frames before computing the derivative. So, some special results are presented to tackle such scenarios, which are presented after the next example.
Example#
The door-wall example is modified to have an additional object: a cat flap \(C\) which makes an angle \(\phi\) with \(\hat{\bf b}_y\).
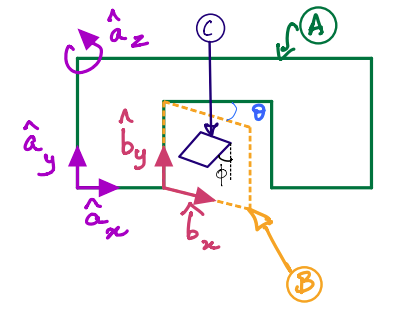
You are asked to compute the angular acceleration of the cat flap \(C\) with respect to \(A\).
Solution
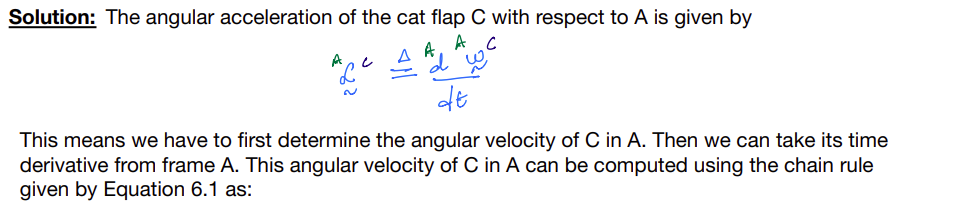

Special results involving time derivatives#
KEY RESULT 1#
As before, \(A\) is a fixed reference frame with unit vectors rigidly attached to it, i.e., \(\hat{\bf a}_i(i=x,y,z)\). Likewise, \(B\) is a rigid body with unit vectors rigidly attached to it, i.e., \(\hat{\bf b}_i(i=x,y,z)\).
\(\bf v\) is an arbitrary vector that is fixed in \(B\) and given in its component form by:
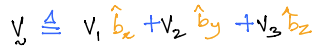
\(v_1, v_2, v_3\) are the scalar components of \(\bf v\) in frame \(B\) and as it is fixed in \(B\) it follows:
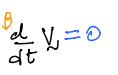

Example#
We will prove key result 1 (boxed in red above) is true for a trivial case: simple rotation.
As before, \(A\) is a fixed reference frame with unit vectors rigidly attached to it, i.e., \(\hat{\bf a}_i(i=x,y,z)\).
Likewise, \(B\) is a rigid body with unit vectors rigidly attached to it, i.e., \(\hat{\bf b}_i(i=x,y,z)\).
\(B\) is hinged to \(A\) such that it is in simple rotation, such that:
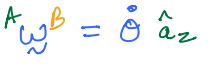
\(\bf v\) is an arbitrary vector that is fixed in \(B\) and given in its component form by: \({\bf v} = v_1\hat{\bf b}_x\)
Prove that:
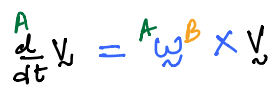
Solution

KEY RESULT 2#
As before, \(A\) is a fixed reference frame with unit vectors rigidly attached to it, i.e., \(\hat{\bf a}_i(i=x,y,z)\). Likewise, \(B\) is a rigid body with unit vectors rigidly attached to it, i.e., \(\hat{\bf b}_i(i=x,y,z)\).

\({\bf v}\) is an arbitrary vector that is moves relative to both \(A\) and \(B\). It is in its component form by:
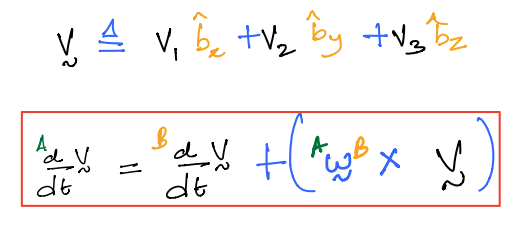
Proof
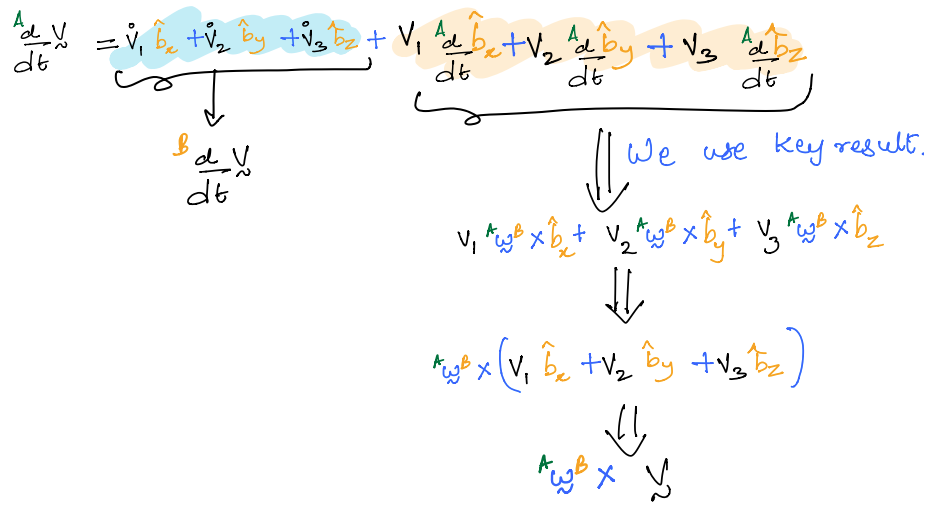
This is a very powerful formula. However, it relies on our ability to derive an expression for the angular velocity vector in an appropriate frame. We will now use it in our cat flap example.
Example#
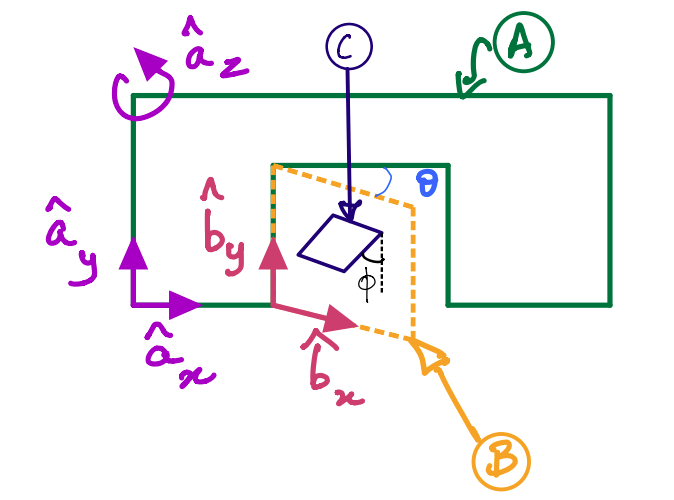
You are asked to find angular acceleration of the cat flap \(C\) with respect to \(A\) using key result 2.
Solution
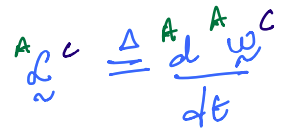
we may then invoke KEY RESULT 2 to rewrite the right hand-side as
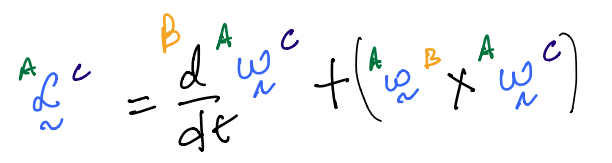
This angular velocity of \(C\) in \(A\) can be computed using the chain rule given by Equation \(6.1\) as: