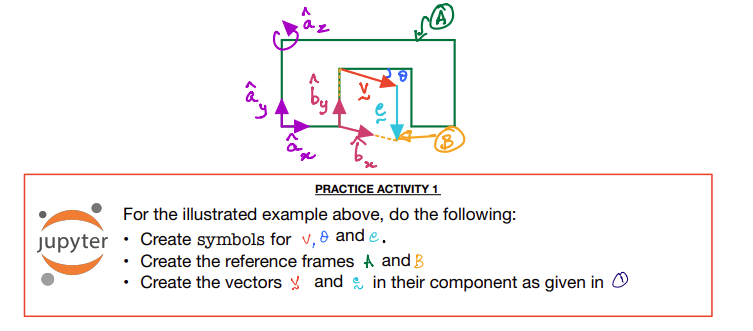
Vectors and Reference Frames for Dynamics: Physical Examples#
Concept

The figure above shows a reference frame \(A\) (in pink) and vector \({\bf v}\) (in black).
Here, \({\bf v}\) is said to be fixed in the frame \(A\) if and only if none of the characteristics of \(\bf v\) (i.e., magnitude and direction) are seen to change when it is observed from \(A\).
Below, we make use of some hand illustrations to exemplify the above concept.
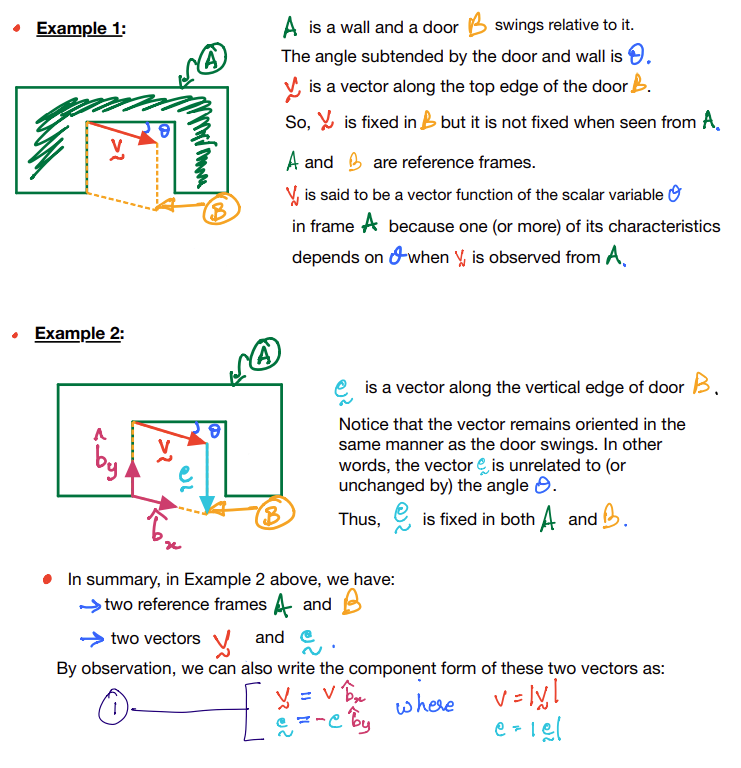
The above handwritten equation can be written in typeface as:
where \(v\) and \(e\) are the magnitudes of \({\bf v}\) and \({\bf e}\).
Notice that we have introduced the unit vectors \(\hat{\bf b}_x\) and \(\hat{\bf b}_y\) for the reference frame \(B\) but \(\hat{\bf b}_z\) is not shown; however, it still does exist and is orthogonal to both \(\hat{\bf b}_x\) and \(\hat{\bf b}_y\). For the sake of the next discussions on how reference frames relate to each other, we now also introduce a right-handed set of unit vectors for frame \( A: \: \hat{\bf a}_x,\;\hat{\bf a}_y\:\&\:\hat{\bf a}_z\). We will work with this example in our next Jupyter Notebook, which is our first Practice Activity specifically pertinent to our discussion on dynamics.